今回の記事では下記のような悩みを解決します。
「重回帰分析というワードをよく目にするので、重回帰分析について知りたい」
「重回帰分析のpythonでの実装方法が知りたい」
早速解説していきます。
重回帰分析とは

重回帰分析は、機械学習の教師あり学習の一つで回帰を実行できます。
具体的に解説します。
説明変数をX1~Xn、目的変数をyとすると、下記の数式で表現できます。
重回帰分析では、データを学習してa0~an (偏回帰係数)を決定し、予測に活用しています。
例えば説明変数が3この場合は、下記のような感じ。
このようにa0~a3が具体的に決定することで、予測できるようになります。
(X1~X3に具体的に数字を入れればyの値は決定されます)
数式が難しくても、「重回帰分析では、データを学習して上記のa0~anを決定し、得られた式を基に予測してるんだ〜」くらいの認識でOKです。
次に重回帰分析の注意点を解説します。
重回帰分析の注意点
重回帰分析を使用する際の注意点を下記に示します。
・多重共線性の影響
それぞれ解説します。
偏回帰係数の解釈
偏回帰係数(a1~an)の値から、どの説明変数(X1~Xn)が目的変数(y)ヘの影響が大きいか一目瞭然ですが、解釈には注意が必要です。
説明変数の取りうる値の範囲次第では、目的変数(y)への影響が変わるため、単に偏回帰係数の大小だけで解釈をしないように注意しましょう。
例えば、下の式では偏回帰係数だけ見ると、X1の偏回帰係数が500と一番大きいので、最も影響が大きいと判断しがちですが、X3の取りうる値が大きいので、X3が目的変数(y)に与える影響が大きいです。そのため、Xの取りうる値の範囲をしっかり確認しましょう。
また、場合によっては説明変数を標準化したりすることも有効です。
0.1 ≦ X1 ≦ 0.2
0.1 ≦ X2 ≦ 0.2
50000 ≦ X3 ≦ 100000
また、予測精度の低いモデルの偏回帰係数を分析しても有益な解析とはならないので、交差検証などで必ず良い精度であることを確認してからにしましょう。
次に多重共線性についてです。
多重共線性の影響を受けてしまう
多重共線性とは、説明変数同士の相関がある状態を言います。
重回帰分析では、多重共線性のある状態で学習すると、算出した偏回帰係数が不安定になります。
そのためモデル構築の際は、事前に2変数の相関やVIF(分散拡大係数)を確認し、相関の大きい説明変数の片方を削除したりする等の対応が必要です。
一方で決定木系モデルは多重共線性の影響を受けません。
(変数重要度を算出する際は影響を受けるが、予測には影響ないです)
重回帰分析は非常に簡単な数式で表現できる一方で、注意すべきことが多いです。
機械学習の目的に応じて是非使い分けてください。
重回帰分析のイメージは掴めたと思うので、次にpythonでの実装について解説します。
重回帰分析の実装

重回帰分析を使用することで、下記のことができます。
・目的変数に対する影響度の高い説明変数の特定(偏回帰係数の算出)
上記2点について、「住宅価格予測の問題」を使用して解説します。
住宅価格予測のデータを簡単に説明すると、’部屋の広さ’や’建築年月日’などの説明変数(79個)を基に住宅価格を予測する問題です。kaggleなどでも予測精度が高くなる手法などが解説されています。
今回はこの住宅価格予測問題を基に、重回帰分析の実装解説をしていきます。
データの準備と前処理
下記のコードでデータをダウンロードできますのでコピペしてダウンロードしてください。
以下dfとします。
(下記コードは特に覚える必要ないのでコピペして活用してください)
from sklearn.datasets import fetch_openml import pandas as pd housing = fetch_openml(name="house_prices", as_frame=True) X = housing.data #説明変数 y = housing.target #目的変数 df = pd.concat([X, y], axis = 1)
説明変数が79個あると解説が難しいので、解説を簡単にするために、説明変数を9個にします。
(予測精度が下がるため、一般的に説明変数をこのように減らすことは本来あり得ませんが、目的は重回帰分析の実装をわかりやすく解説することなのでご容赦ください)
df = df[['YearBuilt', 'YearRemodAdd', 'TotalBsmtSF', '1stFlrSF', 'GrLivArea', 'FullBath', 'TotRmsAbvGrd', 'GarageCars', 'GarageArea', 'SalePrice']]
YearBuilt 建築年月日
YearRemodAdd リフォーム年月日(増改築がない場合は建築年月日と同じ)
TotalBsmtSF 地下室の合計面積(平方フィート)
1stFlrSF 1階面積(平方フィート)
GrLivArea 地上の居住エリアの面積(平方フィート)
FullBath 地上のフルバスルーム
TotRmsAbvGrd 地上の部屋数の合計(バスルームを除く)
GarageCars 車の収容台数に応じたガレージのサイズ
GarageArea ガレージの面積(平方フィート)
このデータを使って解説してきます。
まずは多重共線性の確認をします。
多重共線性の確認
今回は2変数の相関係数を算出し、多重共線性の確認をします。
df.corr( )で確認できます。round(2)で小数点2桁まで算出しています。
‘GarageArea’とGarageCars’、’GriLivArea’と’TotRmsAbvGrd’に高い相関があることが確認できます。
df.corr().round(2)
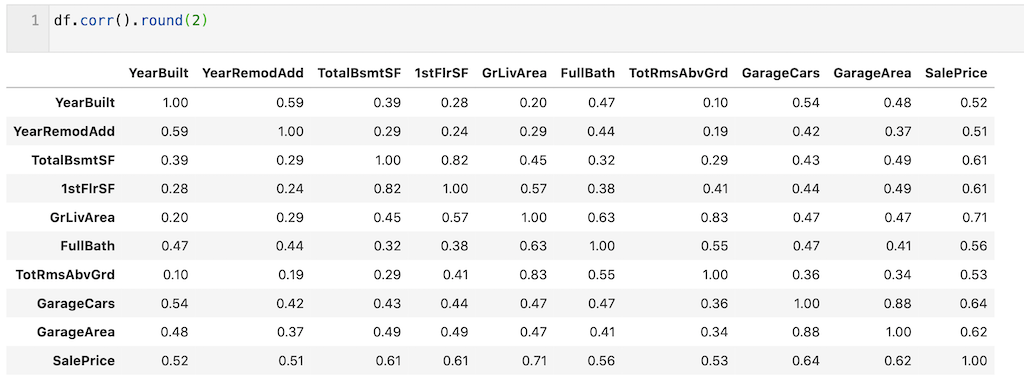
今回は、’GarageCars’と’TotRmsAbvGrd’を削除することとします。
df = df.drop(columns = ['GarageCars','TotRmsAbvGrd'])
これで説明変数の前処理は終了です。
次に目的変数を前処理します。
目的変数の前処理
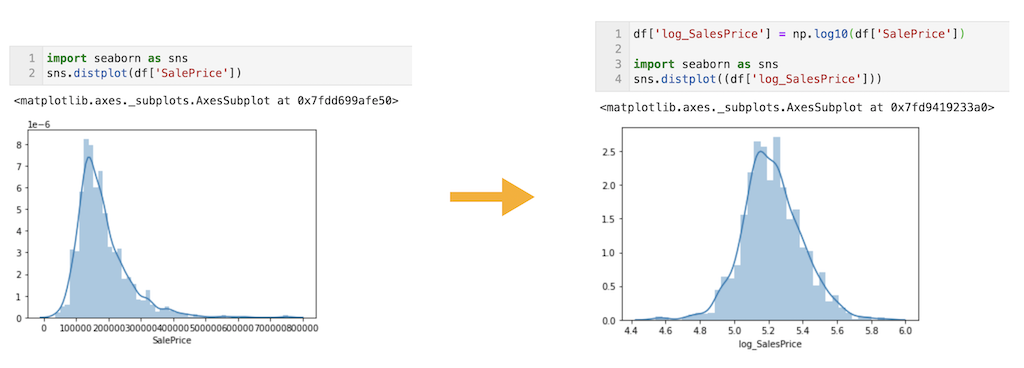
目的変数は対数変換をして使用します。対数変換後の目的変数を’log_SalesPrice’とし、元の’SalePrice’は消去します。
対数変換することで、正規分布に近い形に変換できていることが確認できます。(下記右図)
df['log_SalesPrice'] = np.log10(df['SalePrice']) df = df.drop(columns = ['SalePrice']) import seaborn as sns sns.distplot((df['log_SalesPrice']))
目的変数の前処理はこれで終了です。
最後にデータを分割しておきます。
データの分割
解説のため、dfの1000行目までを訓練データ(df_train)、1000行目以降をテストデータ(df_test)とします。
(本来であれば交差検証で精度を確認します)
df_train = df.iloc[:1000, :] df_test = df.iloc[1000:, :].reset_index(drop = True)
また’log_SalesPrice’列以外を説明変数(X)、’log_SalesPrice’列を目的変数(y)とします。それぞれ訓練(train)、テスト(test)としています。
X_train = df_train.drop(columns = ['log_SalesPrice']) y_train = df_train['log_SalesPrice'] X_test = df_test.drop(columns = ['log_SalesPrice']) y_test = df_test['log_SalesPrice']
データの説明・前処理は以上です。
重回帰分析の実装方法を早速解説していきます。
重回帰分析の学習と予測
モデルの学習はfit( )メソッドで実装できます。
from sklearn.linear_model import LinearRegression model = LinearRegression( ) model.fit(X_train, y_train)
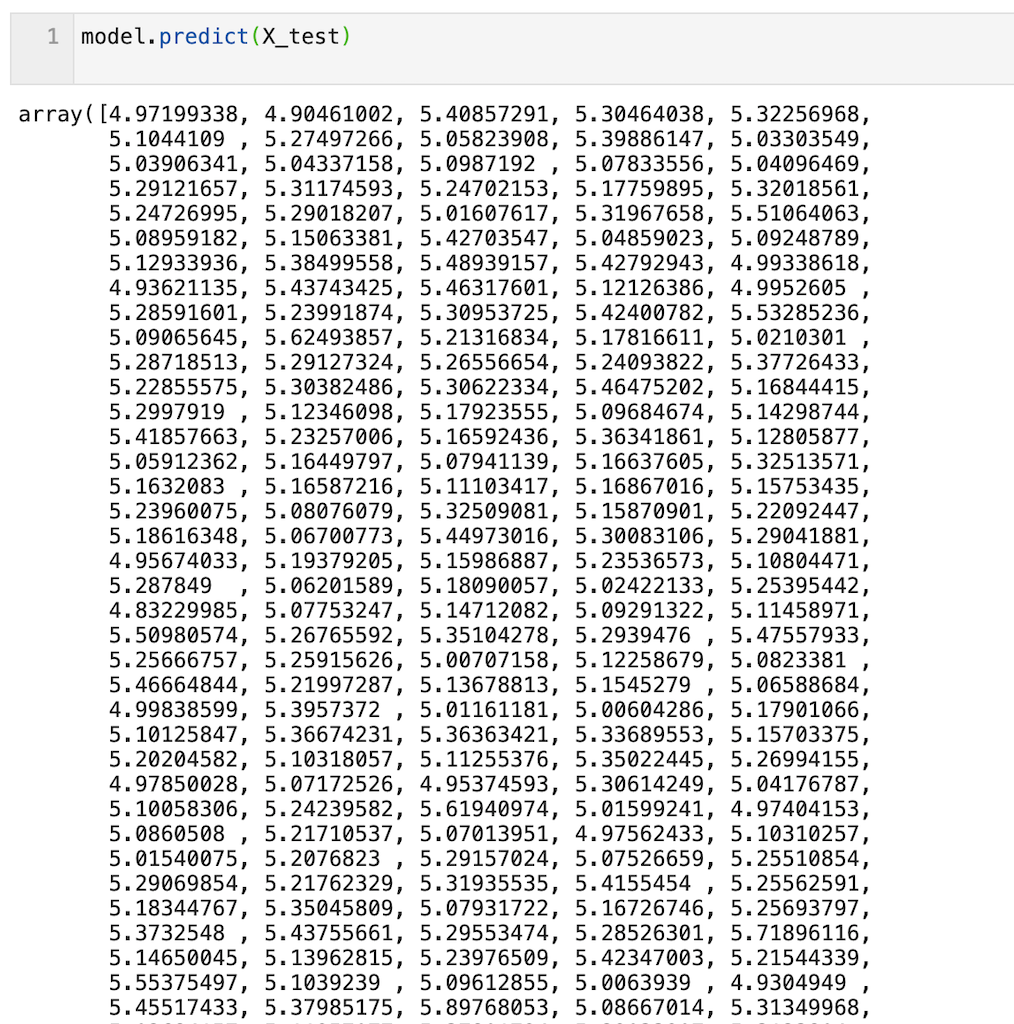
予測はpredict( )メソッドで実装できます。
df_testの460個のデータに対する予測値が出力されていることが確認できます。
model.predict(X_test)
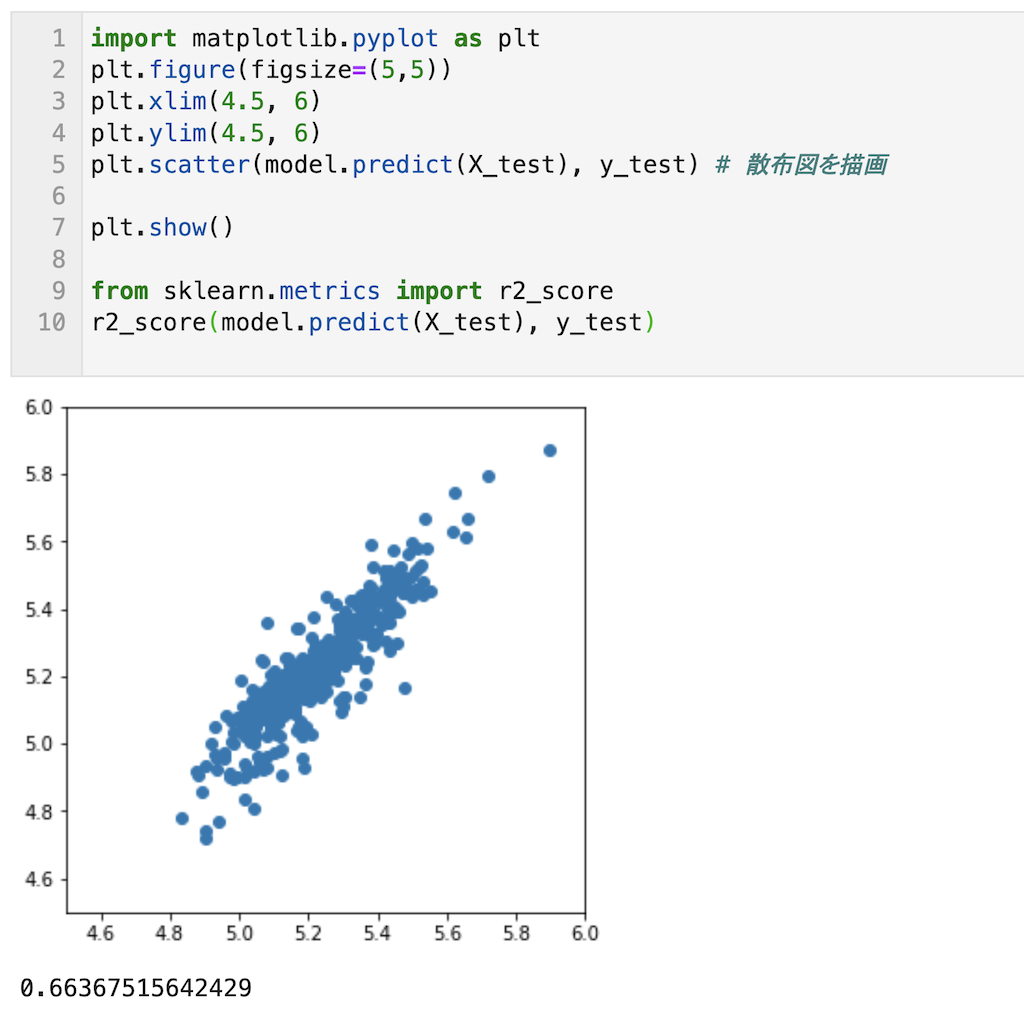
予測結果を算出できたので予測精度を確認してみます。
すべてyの値でy = X上にプロットが載っている事が確認でき、またr2_scoreが0.66とまずまずの結果です。説明変数を増やせば、r2_scoreは0.8程度まで上げれそうです。
import matplotlib.pyplot as plt plt.figure(figsize=(5,5)) plt.xlim(4.5, 6) plt.ylim(4.5, 6) plt.scatter(model.predict(X_test), y_test) # 散布図を描画 plt.show() from sklearn.metrics import r2_score r2_score(model.predict(X_test), y_test)
最後に偏回帰係数の算出について解説します。
偏回帰係数の算出
偏回帰係数の算出はmodel.coef_で算出できます。
今回はモデルをmodelと定義しているため、model.coef_と記載すればOK。
model.coef_

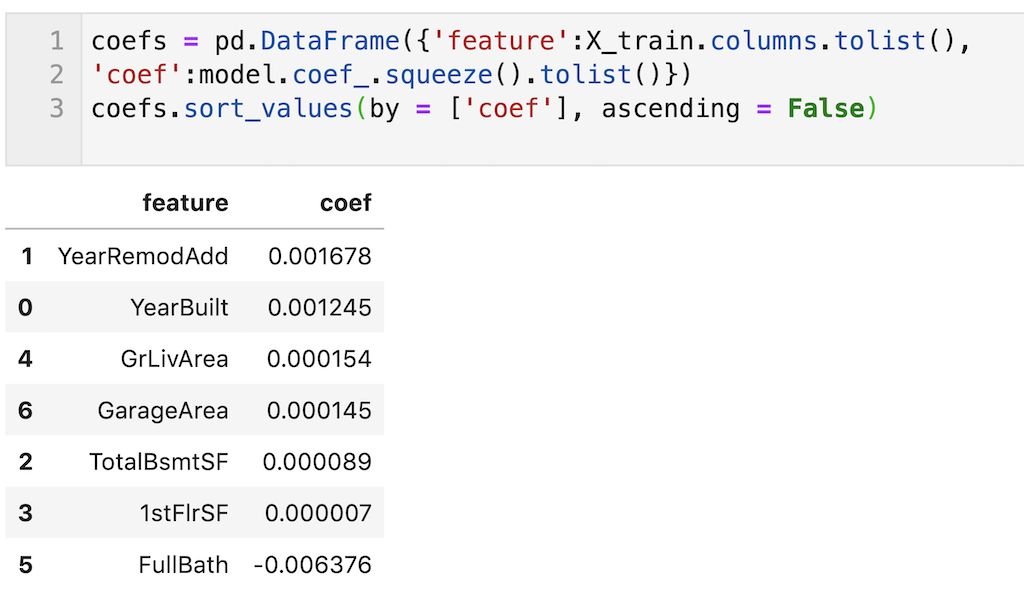
これだとわかりにくいので、説明変数と偏回帰係数を表形式(pandas dataframe)で出力して、数値の大きい順に表記しました。
目的変数を対数変換しているので、偏回帰係数もその分小さくなっています。
coefs = pd.DataFrame({'feature':X_train.columns.tolist(),
'coef':model.coef_.squeeze().tolist()})
coefs.sort_values(by = ['coef'], ascending = False).round(2)
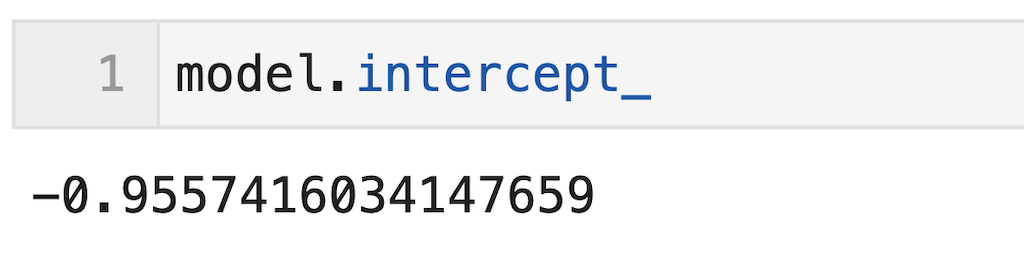
切片はmodel.intercept_で算出できます。
今回はモデルをmodelと定義しているため、model.intercept_と記載すればOK。
model.intercept_
今回はここまでです。最後まで読んでいただきありがとうございます。
重回帰分析はモデルの可読性が高く、最も一般的な機械学習手法です。ですので今回の記事で是非重回帰分析について理解を深めてください。
今回の記事はここまでです。最後まで読んでいただきありがとうございます。
皆さんの機械学習の勉強がさらに進み、理解が深まることを願っています。



