今回の記事では下記のような悩みを解決します。
「決定木というワードをよく目にするので、決定木について知りたい」
「pythonで決定木を使用してモデル構築したい」
「データを学習して構築した決定木を可視化したい」
「変数重要度を算出する方法が知りたい」
早速解説します。
決定木とは

決定木は、yes(True) またはNo(False)で条件分岐する手法で、回帰問題と分類問題の両方に対応しています。
例えば、タイタニック生存者予測問題を例にして、決定木を作成してみます。
下記の決定木に従うと、例えば、「女性」でかつ、「乗客クラスが1等」であれば、生存と出力(予測)できます。
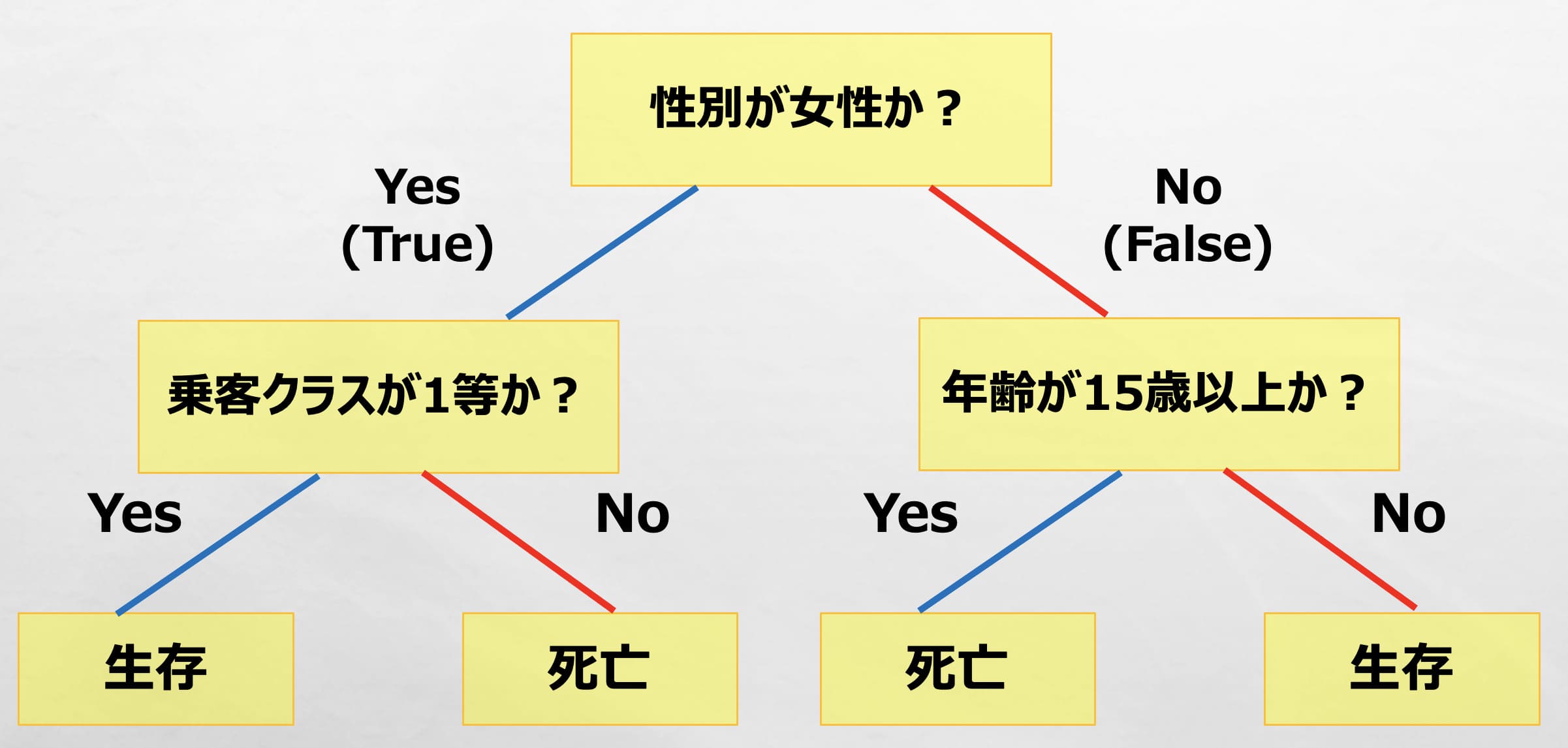
このように決定木を作成することで、条件と結果の関係を可視化したり、予測に活用したりできます。
また回帰の場合は、「生存」、「死亡」の箇所が連続値(数字)になります。
難しい数学を理解できなくても、「決定木モデルでは、データを学習して、このような木をコンピュータで作成して予測に活用してるんだ〜」くらいでOKです。
pythonでの決定木モデルの実装

決定木モデルを活用することで、下記のことができます。
・変数重要度の算出
・構築した決定木の可視化
今回は、上記の点を「タイタニック予測問題」を使用して解説していきます。
タイタニック予測問題はkaggleのホームページからダウンロードできます。

train.csvをdfとして読み込んで、下記のように前処理したデータを使用します。
前処理を簡単に説明すると、’Pclass’,’Age’,’SibSp’,’Parch’,’Fare’,’Sex’,’Embarked’の7個の説明変数を使用し、’Age’列の欠損値を平均値、’Embarked’列の欠損値を最頻値で補完し、カテゴリカル変数をダミー変数化しています。
(今回は前処理が目的ではないので、わからなくても全く問題ないです。コピペして次に進んでください!)
#データの前処理 #今回使うカラムを抽出 df = df[['Pclass','Age','SibSp','Parch','Fare','Sex','Embarked','Survived']] #欠損値補完 Age列は平均、Embarked列は最頻値で補完 df['Age'] = df['Age'].fillna(df['Age'].mean()) df['Embarked'] = df['Embarked'].fillna(df['Embarked'].mode()[0]) #ダミー変数化 df = pd.get_dummies(df, drop_first = True) #dfを出力 df
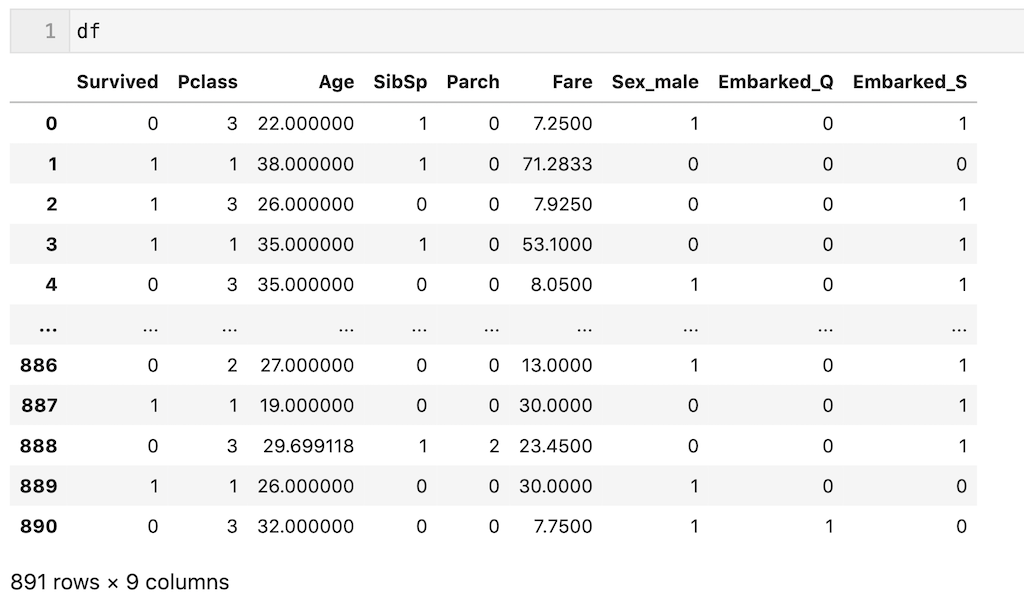
また今回は、dfの700行目までを訓練データ(df_train)、700行目以降をテストデータ(df_test)とします。
df_train = df.iloc[:700, :] df_test = df.iloc[700:, :]
また’Survived’列以外を説明変数(X)、’Survived’列を目的変数(y)とします。それぞれ訓練(train)、テスト(test)としています。
X_train = df_train.drop(columns = ['Survived']) y_train = df_train['Survived'] X_test = df_test.drop(columns = ['Survived']) y_test = df_test['Survived']
データの説明と前処理は以上です。
次は、pythonで決定木モデルを実装する方法を解説していきます。
決定木モデルの学習
決定木モデルの学習は下記コードで実行できます。
タイタニック予測は分類問題なのでDecisionTreeClassifierを使用。
回帰の場合はDecisionTreeRegressorを使用する。
from sklearn.tree import DecisionTreeClassifier model = DecisionTreeClassifier() model.fit(X_train, y_train)
続いて構築した決定木モデルを用いて予測してみます。
決定木モデルで予測
上で構築した決定木モデル(model)を用いてテストデータ(X_test)を予測する場合は下記コードで実行できます。
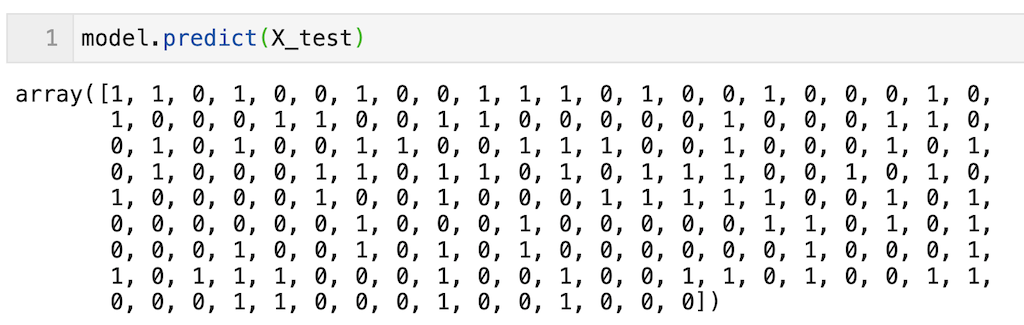
191個のデータに対する予測が実行できている(0 or 1が出力されている)ことが確認できる。
model.predict(X_test)
決定木モデルの学習と予測ができたので、次は「調整すべきハイパーパラメータ」のお話。
決定木モデルで調整すべきハイパーパラメータ
調整すべきハイパーパラメータは「木の深さ(max_depth)」です。
木の深さは、深くするほど良いじゃないか!と言われそうですが、木の深さを深くするほど学習データに過剰に適合(過学習)しやすくなります。なので、学習不足にならず、かといって過学習しない適切な『木の深さ』に設定することが大切です。
汎化性能を確認しながら、max_depthの値を決定します。
今回は決定木を見やすく可視化したいので「max_depth = 3」としてみます。
(max_depthの値が大きすぎると、決定木が複雑になるので)
from sklearn.tree import DecisionTreeClassifier model = DecisionTreeClassifier(max_depth = 3) model.fit(X_train, y_train)
続いて「構築した決定木モデル」を可視化してみます。
構築した決定木モデルの可視化
今回は、graphvizを用いて決定木を可視化してみます。
graphvizはデフォルトでanacondaに入っていないのでインストールする必要があります。
下記のコマンドでダウンロードできます。
conda install anaconda::graphviz
graphvizを使って構築した決定木を可視化してみます。
「max_depth = 3」としているので木の深さが3になっています。
from sklearn.tree import DecisionTreeClassifier
model = DecisionTreeClassifier(max_depth = 3)
model.fit(X_train, y_train)
from sklearn.tree import export_graphviz
import graphviz
dot_data = export_graphviz(model, out_file = None,
feature_names = X_train.columns,
class_names = ['Died', 'Survived'],
filled = True, rounded = True,
special_characters = True)
graph = graphviz.Source(dot_data)
graph.view( )
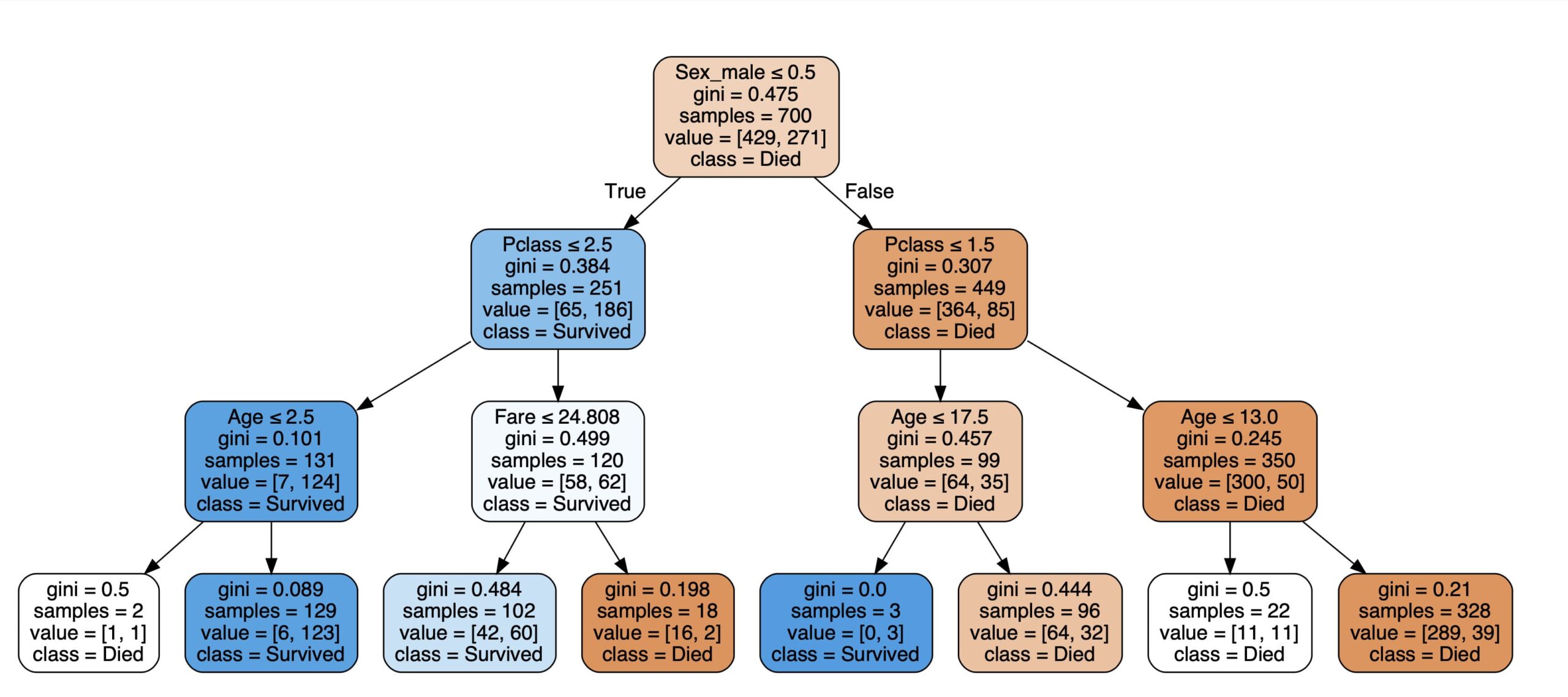
出力された決定木を見てみると、Yes(True)またはNo(False)が3回行われて出力されている(max_depth = 3)ことが確認できます。
またSurvivedとDiedが完全に分割できていないことが確認できます。完全に分類できていないところは、多数決により出力が決定されます。
今回は決定木の見やすさ優先のため、max_depth = 3としていますが、予測精度の観点からも、もう少し深い木構造にしたほうがいいと思います。
(練習として是非やってみてください!)
少しだけ決定木について補足
決定木モデルの構築(学習)では、「ジニ不純度」を最小化することが目標です。
上の画像で「gini」がジニ不純度を表しています。
ジニ不純度の最小化というと難しいですが、要は「Survived」と「Died」を完全に分割した状態(Survivedだけ、Diedだけの状態)を目指しているということです。
出力した決定木を確認すると、giniの数値が0より大きいところは、完全に分割できていないことが確認できると思います。
また、ジニ不純度を最小化する上で、下記を決定しています。
・どの基準で分割するか(しきい値やルールを決める)
少し難しい説明をしましたが、わからなければ「データを学習して、可能な限り、SurviedとDiedを完全に分割できる木を目指しているんだ〜」くらいの理解度でOKです!
最後に重要度の算出です。
重要度の算出
重要度の算出はfeature_importances_で算出できます。
今回は決定木のモデルをmodelと定義しているため、model.feature_importances_と記載すればOK。
今回はmax_depth = 3なので重要度0の説明変数があります(木が深くないので使用されていない説明変数がある)が、max_depthの値を変えると(大きくすると)、重要度の値も変わってきますので、是非練習としてやってみてください。
model.feature_importances_

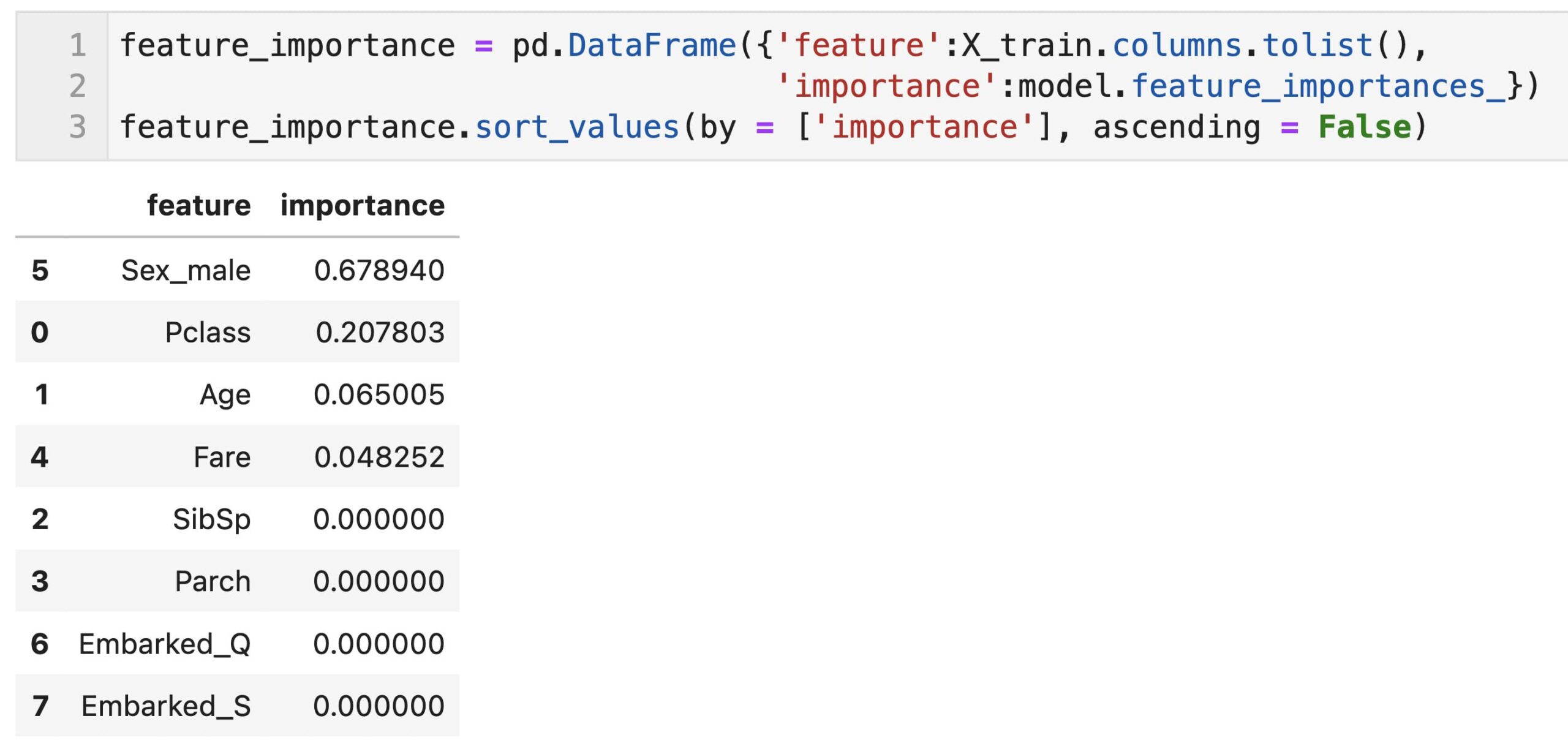
これだとわかりにくいので、説明変数と重要度を表形式(pandas dataframe)で出力して、変数重要度の大きい順に表記しました。
今回構築したモデルは、Sex_maleとPclassの重要度が大きい結果となっていることが確認できます。
feature_importance = pd.DataFrame({'feature':X_train.columns.tolist(),
'importance':model.feature_importances_})
feature_importance.sort_values(by = ['importance'], ascending = False)
変数重要度の注意点
最後に少しだけ注意点を書きます。
変数重要度では説明変数が正・負、どちらに効果があるのかわからない
重回帰分析では偏回帰係数の符号から、その説明変数が正に働いているのか、負に働いているのか、わかるが、変数重要度では正・負、どちらに効果があるのかわかりません。あくまで「どの説明変数が寄与しているのか」くらいしかわかりません。
精度の良いモデルを作らないと変数重要度の議論ができない
変数重要度の大きさは、「モデル構築時にどれだけその説明変数が寄与しているのかという寄与度」であるため、精度の高いモデルを構築できなければ、変数重要度は意味をなさない。精度の低いモデルの変数重要度を議論することに意味はないから。そのため、変数重要度を議論する際は、モデルの精度を確認してからにしましょう。
今回の記事はここまでです。最後まで読んでいただきありがとうございます。
皆さんの機械学習の勉強がさらに進むことを願っています。



