今回の記事では下記のような悩みを解決します。
「ロジスティック回帰というワードをよく目にするので、ロジスティック回帰について知りたい」
「ロジスティック回帰のpythonでの実装方法が知りたい」
早速解説していきます。
ロジスティック回帰分析とは

ロジスティック回帰分析は、機械学習の教師あり学習の一つで分類タスクを実行できます。
具体的に解説します。
説明変数をX1~Xn、目的変数をyとすると、ロジスティック回帰は下記の数式で表現できます。
①の式をシグモイド関数と呼び、yの取りうる値の範囲は0~1の間になります。(下記グラフがシグモイド関数の出力結果ですが、縦軸を見ると取りうる値が0~1になっていることが確認できます)
②は重回帰分析の数式です。
ロジスティック回帰分析では、重回帰分析の数式をシグモイド関数に当てはめ、yの取りうる値の範囲を0〜1の間にし、「y < 0.5なら0と出力し、y > 0.5なら1と出力」することで分類してます。
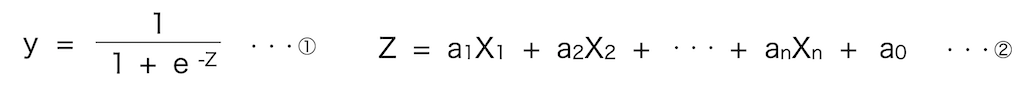
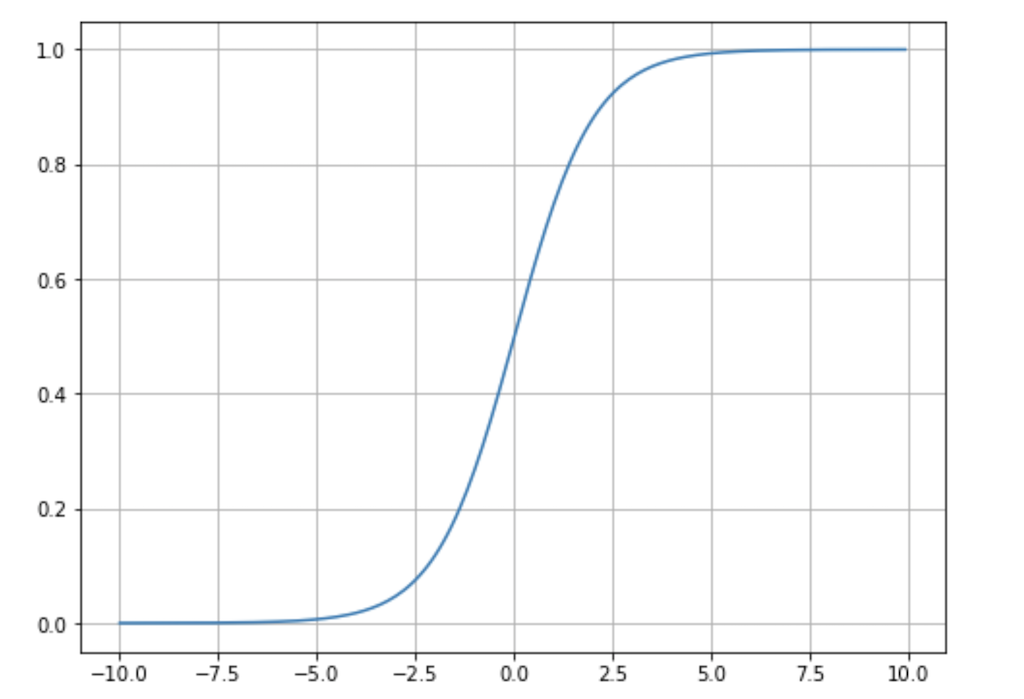
数式が難しくても、「ロジスティック回帰では、データを学習して上記のa0~anを決定し、得られた式を基に0 or 1と予測してるんだ〜」くらいの認識でOKです。
ロジスティック回帰は、数式で表現でき、モデルの可読性が高いため、データサイエンスでは非常に有用な手法となりますので是非理解してください。
次に決定木系モデルとの違いについて解説します。
決定木系モデルとの違い
決定木系モデルとの違いを下記に示します。
・多重共線性の影響を受けてしまう
偏回帰係数を算出できる
決定木系モデルでは変数重要度を算出できるが、正負の影響やどの程度目的変数に影響を与えるのか直感的にわかりにくい問題があります。一方、ロジスティック回帰は、偏回帰係数の大小、正負の符号から説明変数が目的変数に与える影響が直感的にわかりやすいため、モデルの可読性に優れています。
多重共線性の影響を受けてしまう
一方でロジスティック回帰は「Z = a1x1 + a2x2 ・・・ + anxn+a0」が重回帰分析の数式なので多重共線性の影響を受けます。なので使用する際は、説明変数間の相関を確認する必要があります。一方で決定木系モデルは多重共線性の影響を受けません。(変数重要度を算出する際は影響を受けるが、予測には影響ないです)
そのため、機械学習の目的に応じて使い分ける必要があります。
ロジスティック回帰のイメージは掴めたと思うので、次にpythonでの実装について解説します。
ロジスティック回帰の実装

ロジスティック回帰を使用することで、下記のことができます。
・偏回帰係数の算出
上記2点について、タイタニック予測問題を使用して解説します。
今回は解説を簡単にするために、前処理後のデータ(df)を使用します。一応前処理を簡単に説明すると、’Plass’、’Age’、’SibSp’、’Parch’、’Fare’、’Sex’、’Embarked’の7個の説明変数を使用し、欠損値を平均値、最頻値で補完し、カテゴリカル変数をダミー変数化しています。今回は前処理が目的ではないので、わからなくても全く問題ないです。
dfを下記に示します。
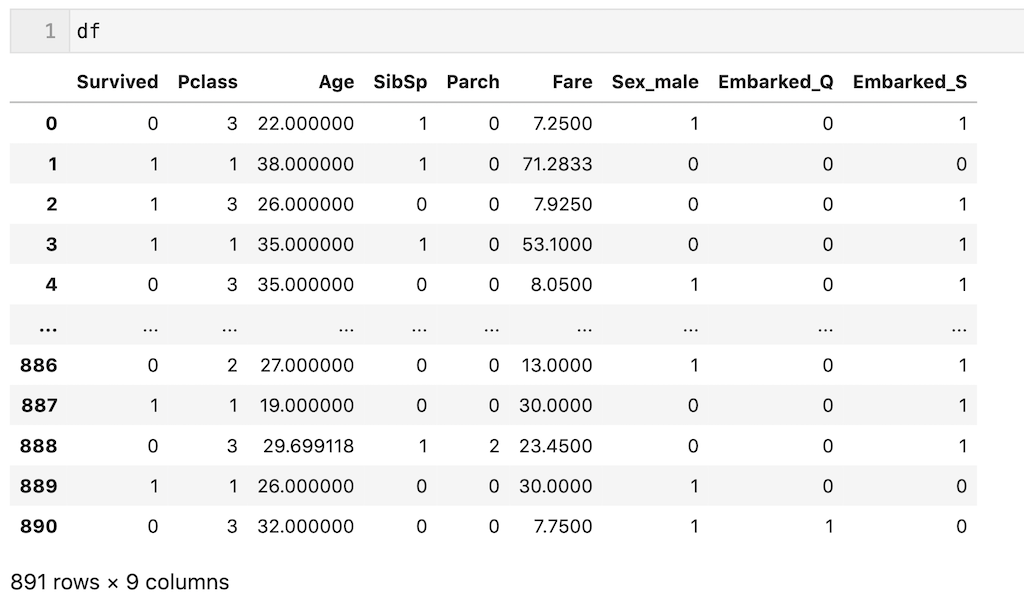
解説のため、dfの700行目までを訓練データ(df_train)、700行目以降をテストデータ(df_test)とします。
df_train = df.iloc[:700, :] df_test = df.iloc[700:, :]
また’Survived’列以外を説明変数(X)、’Survived’列を目的変数(y)とします。それぞれ訓練(train)、テスト(test)としています。
X_train = df_train.drop(columns = ['Survived']) y_train = df_train['Survived'] X_test = df_test.drop(columns = ['Survived']) y_test = df_test['Survived']
データの説明は以上です。
モデル構築の前に、説明変数間の相関係数を確認します。
‘Survived’は目的変数なので関係ないのですが、’Pclass’から’Embarked-S’まで、相関係数がそこまで大きくないので、説明変数はこのまま全部使用してモデル構築します。
(一般的に相関係数が0.8以上あれば多重共線性の影響が出てくると言われることが多いです。)
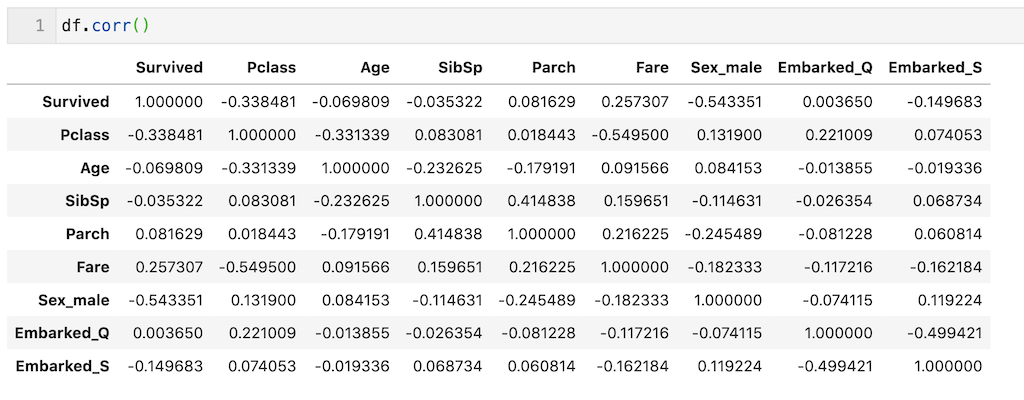
ロジスティック回帰の実装方法を早速解説していきます。
ロジスティック回帰の学習と予測
モデルの学習はfit( )メソッドで実装できます。
from sklearn.linear_model import LogisticRegression model = LogisticRegression( ) model.fit(X_train, y_train)
予測はpredict( )メソッドで実装できます。
df_testの191個のデータに対する予測(0 or 1が出力されている)を実行できていることが確認できます。
model.predict(X_test)
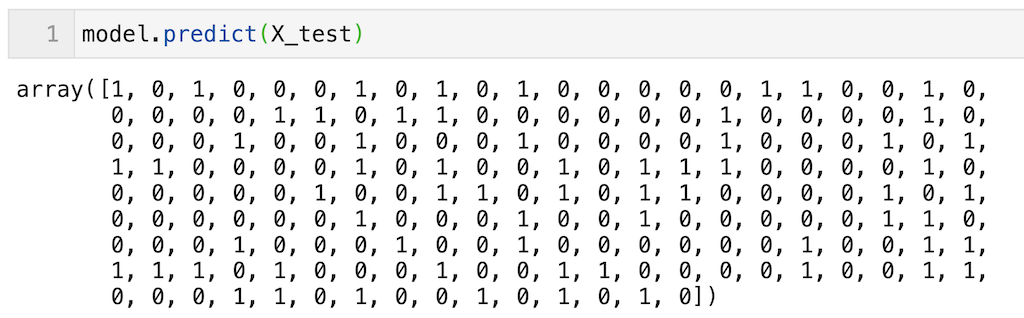
predict_proba( )メソッドを使用することで、「0となる確率、1となる確率」を算出できます。
ただしそのまま出力すると0となる確率、1となる確率どっちも出力するので見にくいです。
model.predict_proba(X_test)
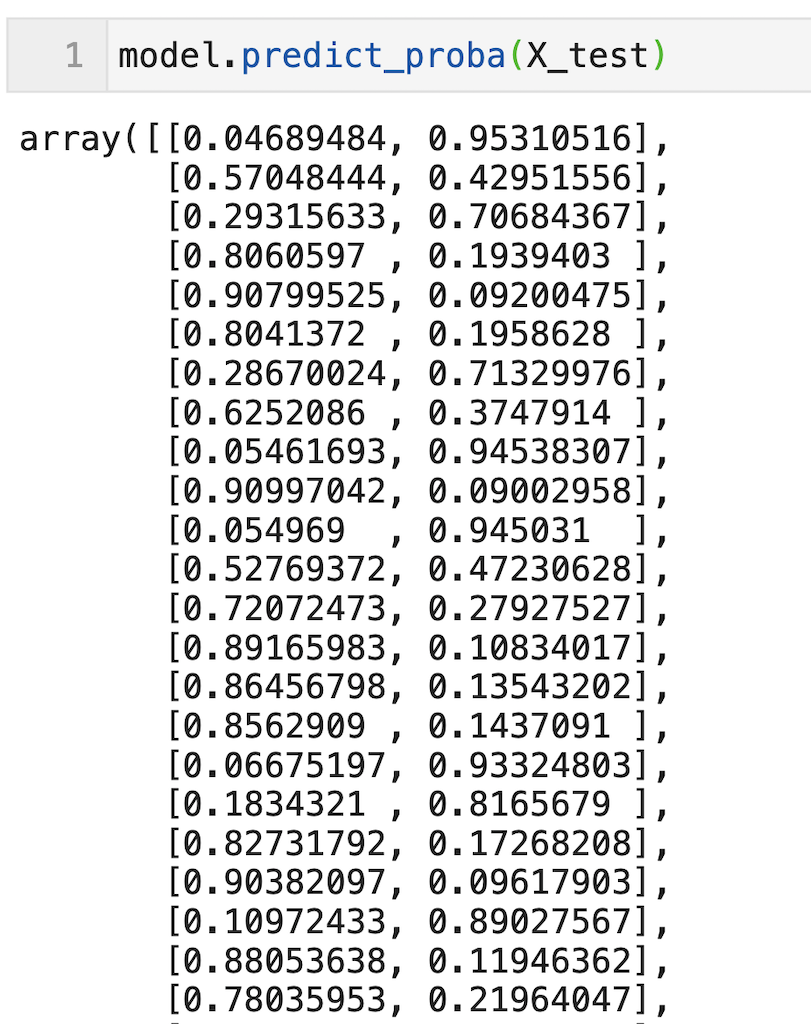
そこで今回は「1となる確率」のみを出力するコードを例として示しますので、コピペして使ってみてください。こちらの方が見やすいです。
1となる確率なので、「0.5より小さいと0、0.5より大きければ1」と出力されます。
今回は見やすさのため.round(2)として小数点2桁まで記載しています。
model.predict_proba(X_test)[:,1].round(2)
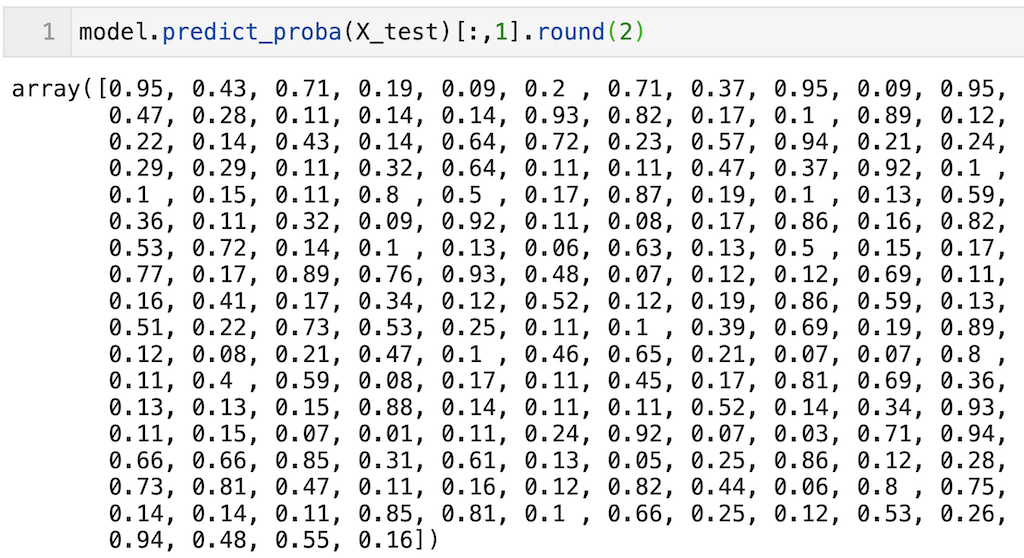
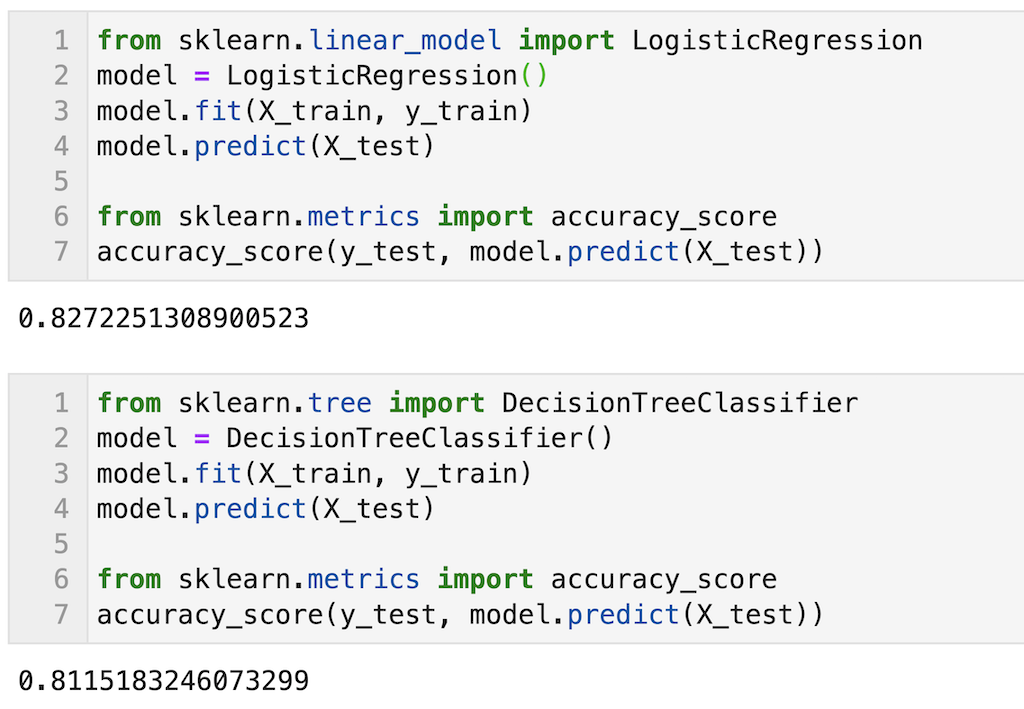
参考程度に同じデータを使って決定木と予測精度の比較を示します。
正解率を算出していますが、今回の場合は少しロジスティック回帰の方が正解率が高いです。
次にハイパーパラメータについて解説します。
調整すべきハイパーパラメータ
一般的によく調整されるハイパーパラメータを下記に示す。
書き方の参考のために、コードを下記に示します。
例としてC = 2としてみます。参考程度に正解率の結果も示しますが、少し正解率が下がりました。適切にハイパーパラメータを調整する必要があることを確認いただけると思います。
from sklearn.linear_model import LogisticRegression model = LogisticRegression(C = 2) model.fit(X_train, y_train)

最後に偏回帰係数の算出について解説します。
偏回帰係数の算出
偏回帰係数の算出はmodel.coef_で算出できます。今回はモデルをmodelと定義しているため、model.coef_と記載すればOK。
model.coef_

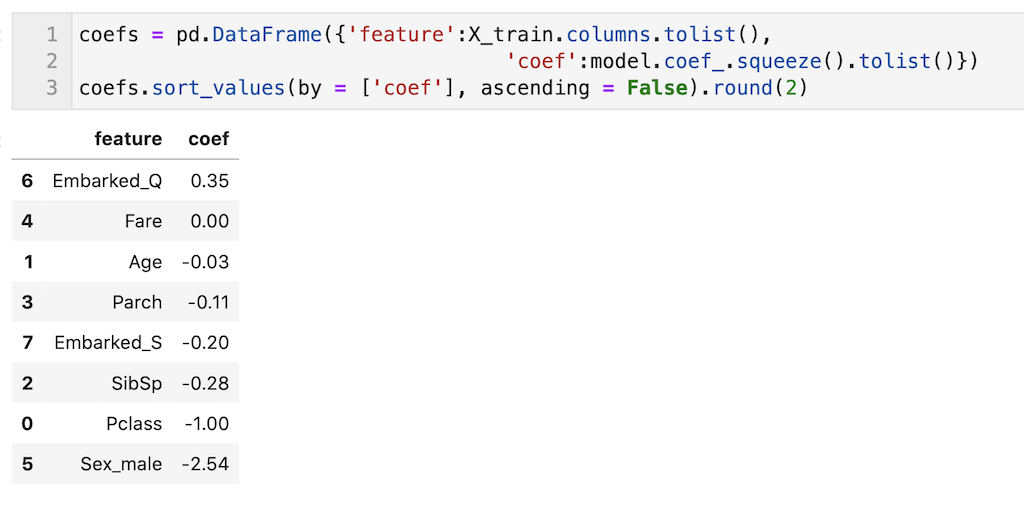
これだとわかりにくいので、説明変数と偏回帰係数を表形式(pandas dataframe)で出力して、数値の大きい順に表記しました。
今回のモデルでは、’Sex_male’の偏回帰係数が-2.54とかなり大きく、男性の場合はyが0に近づく(殆ど生存しないだろう)ことがわかります。(いつの世も女性ファーストで、男の皆さんかっこいいです!!)
決定木系のモデルとは異なり、偏回帰係数を算出できることで、モデルの可読性が高くなるのがロジスティック回帰のいいところです。
coefs = pd.DataFrame({'feature':X_train.columns.tolist(),
'coef':model.coef_.squeeze().tolist()})
coefs.sort_values(by = ['coef'], ascending = False).round(2)
今回はここまでです。最後まで読んでいただきありがとうございます。
ロジスティック回帰はモデルの可読性が高く、実社会のデータ分析では非常に重宝される手法です。ですので今回の記事で是非ロジスティック回帰について理解を深めてください。
今回の記事はここまでです。最後まで読んでいただきありがとうございます。
皆さんの機械学習の勉強がさらに進み、理解が深まることを願っています。



